Git を永続データ構造として見る
競技プログラミングは役に立つ、 というかアルゴリズムとデータ構造は身の回りで役に立ってるよ案件なんですが、 バージョン管理システム Git のコア部分の仕組みは永続データ構造です。
ブラックボックスとして使うより簡単な仕組みを知ってる方が 親しみやすいと思うので雑に解説します。 "git データ構造" とかでググると同様の話結構出てくる N 番煎じです (というか公式ドキュメントに書いてあるまんまのことを競プロer的に見るとこうなっているよという話。 Git の使い方を解説する記事ではありませんし、まして GitHub は何の関係ありません)。
ソースコードや公式ドキュメントを読み込んだわけじゃないのでテキトーなことが書かれているかもしれません。 公式ドキュメントを読んでください。
ざっくり
- "commit" は登録したファイルを含むディレクトリツリーのスナップショットを保存している
- "commit" はディレクトリツリーを根付き木 (正確にはDAG) として表現する
- 根はコミットのデータ
- 節はディレクトリ
- 葉はファイルのバイナリデータ(deflate圧縮済み) に対応する
- 新たな "commit" で追加/変更されたファイルを子孫に持つ頂点のみが新たに作り直される (ここが永続木 / 永続DAGになってる)
- この永続木のノード (オブジェクト) は
.git/objectsに保持される - コミットグラフは永続木の根を頂点とする DAG になる
という感じです。 だいたい 10.2 Gitの内側 - Gitオブジェクト に書いてあります。
具体例
$ tree .
.
├── Cargo.toml
├── doc
│ └── index.html
├── readme.md
└── src
└── main.rs
$ git add .
$ git commit -m "first commit"
として最初のコミットをしました。
git cat-file -p <object> でオブジェクト(永続木のノード)の内容を確認できます。
$ git cat-file -p head tree 33263cd6b7ffee2b8a73ca34d39d328da0e1d4db author koyumeishi <mail> 1638982920 +0900 committer koyumeishi <mail> 1638982920 +0900 first commit
tree 33263cd... がこのコミットデータが管理するディレクトリツリーの根のオブジェクトです。 object にこの 33263cd... を指定してやればディレクトリツリーを潜って中身を確認できます。
$ git cat-file -p 33263cd 100644 blob b245fd1be890ef1ff1499fa2bfd0e262a3928d1b Cargo.toml 040000 tree c5c076a4875e5de1b8ab45d79bbe22e10d95acd1 doc 100644 blob e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 readme.md 040000 tree 305157a396c6858705a9cb625bab219053264ee4 src
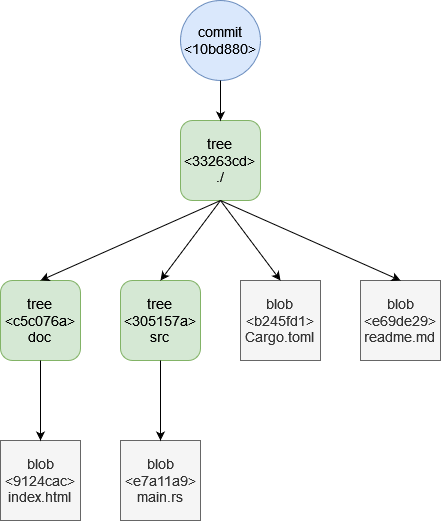
ここで src/main.rs を編集して新たにコミットします。
$ git diff 10bd880
diff --git a/src/main.rs b/src/main.rs
index e7a11a9..9e6acca 100644
--- a/src/main.rs
+++ b/src/main.rs
@@ -1,3 +1,3 @@
fn main() {
- println!("Hello, world!");
+ println!("Hello, world! 😎");
}
$ git cat-file -p head tree f527b85445af1fe88dfd9b3e7c7628cd7edc9069 parent 10bd88083ee76086bbc261e4af93ff83075a7c5b author koyumeishi <mail> 1638985276 +0900 committer koyumeishi <mail> 1638985276 +0900 second commit
$ git cat-file -p f527b85 100644 blob b245fd1be890ef1ff1499fa2bfd0e262a3928d1b Cargo.toml 040000 tree c5c076a4875e5de1b8ab45d79bbe22e10d95acd1 doc 100644 blob e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 readme.md 040000 tree 8323f5ec98f225298d3a0fbde5f2899ebe382a51 src
ディレクトリツリーを図示するとこうなります。

変更した main.rs を子孫にもつオブジェクトのみ新たに作り直されます。
過去のコミットに存在したオブジェクトも .git/objects にそのまま残るので、
ディレクトリツリーの根となるオブジェクト(= コミット) を指定すれば、
オブジェクトを辿ってディレクトリツリーのスナップショットを復元できます。
これが "Git は永続木" という話。 厳密にはハッシュ値が一致するバイナリのオブジェクトは一つしか作られないので、 丸々コピーしたファイルが複数存在してたりすると木ではなく DAG になります。
次に "コミットグラフは上の永続木の根を頂点とするDAG" という話。
コミットデータには、そのコミットの親コミットを指す parent オブジェクトの値も含まれていて、コミットオブジェクトをグラフとして図示すると DAG になります。

これで Git のコア部分を永続データ構造として解釈できたと思います。 以下見えてくるもの。
git はただスナップショットを保持するものなので、管理するデータはテキスト形式に限らない
変更されたファイルはコミット毎に完全な状態で保存されるので、 大きなデータを何度も変更するとリポジトリが肥大化しそう? ( Packfile という差分圧縮機能もあって時折圧縮してくれるみたい。 差分取るのが難しいタイプのバイナリデータは厳しそう)
branchはコミットグラフの DAG 上の一連の頂点を示しているだけの概念。

mergeは異なるスナップショットを合成するだけの機能。
マージ元とマージ先で同じファイルを編集していなければ普通に合成ができるはずだし、 同じファイルを編集してしまっていた場合は通常コンフリクトします。 (git がよしなにしてくれる場合もある)リポジトリはコミットグラフのインスタンス。一部や全部をコピーしたりされたりの関係。

repository
GitHub や Bitbucket はそのインスタンスを保存しておいてくれる上に周辺が便利になる機能を提供してくれてるありがたいサービス。どうしてファイルを差分じゃなくて完全な状態で保存するの?無駄では?
-> 知らない。 冗長性とか、ストレージやネットワークの大容量化とか、最新のコミットだけ取ってくるときにうれしいとか?
以前書こうとして下書きにずっと眠ってた記事を掘り起こしました。
業プロer的には当然のお話も新進気鋭学生競プロerは知らなかったりするかもなので念のため清書。途中で飽きて「この図に何の意味が…?」みたいな図あるような気もする。
バージョン管理システムは短時間コンテストではそんな意味ないけど、ライブラリ管理や
マラソン (ヒューリスティックコン) なんかでは役に立つと思うので使ったことない方は是非挑戦してみてください。
色んな機能を使いこなそうとすると大変だけど、コア部分だけ利用するなら結構簡単です。
おしまい。